قابلية القسمة (Divisibility) على الأعداد الأساسية

تُعد قواعد قابلية القسمة Divisibility Rules من أهم الأساسيات في علم الرياضيات، حيث تساعد الطلاب على التحقق بسرعة مما إذا كان العدد يقبل القسمة على عدد آخر بدون الحاجة لإجراء عملية القسمة الكاملة. فيما يلي نستعرض القواعد الخاصة بالقسمة على الأعداد (2، 3، 4، 5، 6، 10) كل واحدة على حدة:-

1- قابلية القسمة على 2 (Divisibility by 2):-

اى عدد يقبل القسمة على 2 اذا كان عدد زوجيا (even digits: 0, 2, 4, 6, 8) فمثلا الاعداد 120،324،562،926،158 هى اعداد تقبل القسمة على 2 وذلك لان رقم الآحاد يحتوى على عدد زوجى وبالتالى فان العدد الزوجى الذى رقم آحاده عددا زوجيا فانه يقبل القسمة على 2.

2- قابلية القسمة على 3 (Divisibility by 3):-

3- قابلية القسمة على 4 (Divisibility by4):-

يقبل العدد القسمة على 4 اذا توفر احد شرطين :-

1- اذا كان رقما الآحاد والعشرات يحتوى على اصفار مثل 100،1500،600،…………….

2- او ان يكونا عددا يقبل القسمة على 4 مثل 512،716،924،832،………………..

4- قابلية القسمة على 5 (Divisibility by5):-

يقبل العدد القسمة على 5 اذا كان رقم أحاده 0 او 5 مثل 100،155،345،320،…………..

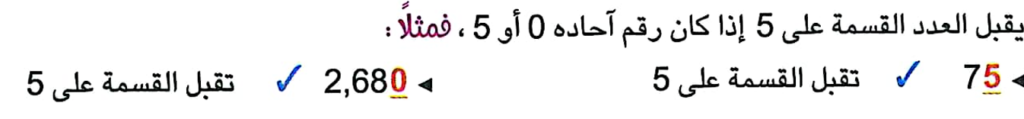
5- قابلية القسمة على 6 (Divisibility by6):-

العدد يكون قابلاً للقسمة على 6 إذا كان:-

1- divisible by 2 (أي عدد زوجي).

2- divisible by 3 (مجموع أرقامه يقبل القسمة على 3).

ملحوظة : لابد ان يتوفر فيه الشرطان معا.

مثال:

1. العدد 132 → عدد زوجي + (1 + 3 + 2 = 6 يقبل القسمة على 3) → إذن 132 divisible by 6.
2. العدد 124 → زوجي (ok) لكن (1 + 2 + 4 = 7 لا يقبل القسمة على 3) → ليس divisible by 6.

6-القسمة على 10 (Divisibility by 10):-

يقبل العدد القسمة على 10 اذا كان رقم آحاده 0 مثل 50 ، 70 ،120،1550،………….

الخلاصة : قواعد قابلية القسمة Divisibility Rules أداة ذكية لتسهيل الحسابات، فهي تختصر الوقت والجهد وتساعد في التحقق السريع من نتائج العمليات. إتقان هذه القواعد يُعد أساسًا قويًا للطلاب في تعلم الحساب الذهني Mental Math وتنمية مهارات التفكير الرياضي.